Aspects physiques

Pour les besoins de cette expérience, nous allons faire l'hypothèse que les spins des deux premiers niveaux excités de même que les spin et parité de l'état fondamental du ⁶⁰Ni sont connus (Schéma de désintégration du ⁶⁰ Co Fig.1). Pour déterminer la parité des niveaux excités, il s'agira d'établir le caractère magnétique ou électrique des deux radiations émises par les deux niveaux lors de leur désintegration vers l'état fondamental. Ceci est accompli par la mesure de la polarisation linéaire p des deux . Les radiations ont des énergies de 1173 keV et de 1333 keV, respectivement.

A tout sont associés des vecteurs de champ électrique et magnétique. La polarisation p correspond au rapport des intensités des ayant leur vecteur électrique parallèle au "plan de la réaction", et perpendiculaire à ce plan, .

Cependant, nous mesurons les quantités et qui nous donnent les intensités des diffusés dans les plans, parallèle et perpendiculaire respectivement, par rapport au plan de la réaction. Ces quantités mesurées sont reliées aux valeurs de et par les sections efficaces de Klein-Nishina, et qui donnent la probabilité de diffuser des dans les plans parallèle et perpendiculaire i.e.

et

La relation entre la valeur recherchée p et la valeur mesurée est

où est le rapport d'asymétrie. Pour des détecteurs ponctuels, ce rapport peut se calculer facilement à partir des sections efficaces connues théoriquement. En pratique, il faut utiliser des détecteurs ayant des dimensions finies qui affectent la valeur de ce rapport. Un logiciel a été developpé qui nous permet de calculer ce rapport connaissant les dimensions de nos détecteurs. Le résultat est :

et

Les rayons émis lors de la désintegration des niveaux excités ont une distribution en intensité dans l'espace (appelée corrélation angulaire) décrite par la relation suivante :

La polarisation p des peut être exprimée en termes des coefficients des polynômes de Legendre . Pour une transition E2 nous avons, à = :

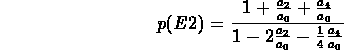
et pour une transition M2 :

Les spins des trois états en jeu étant J=4,2 et 0, respectivement, il est possible de calculer les coefficients avec une grande précision. Pour des détecteurs ponctuels, nous avons pour des transitions J=4 J=2 J=0,

En pratique, les détecteurs utilisés ont un angle solide qui atténue la corrélation angulaire et donc la polarisation linéaire. Cet effet géometrique se manifeste sous l'apparence de facteurs d'atténuation tel que

Dans notre géometrie, deux détecteurs interviennent dans la mesure de la corrélation angulaire, un NaI de
x à 15.5 cm de la source, dont les facteurs d'atténuation ont les valeurs =0.984, =0.948 et un BGO de x à 8.3 cm ayant des valeurs =0.897, =0.685. Dans les calculs, on pourra faire l'hypothèse que les coefficients n'ont pas d'erreur tandis que les coefficients ont des erreurs de l'ordre de 2% sur et 4% sur .